Test d'hypothèsesEléments fondamentaux de la statistique inférentielle. Statistique non paramétrique, modèle linéaire, analyse de la variance, rapports de vraisemblance. |
|
Tests du Khi2 Loi du ${chi}^2$ et statistique du khi2. Test d'ajustement à une distribution connue. Test d'ajustement à une distribution inconnue. La question des degrés de liberté. Khi2 d'une table de contingence. Tests exacts. |
|
Rapports de vraisemblance Aucun sommaire |
|
Risques, puissance et robustesse Aucun sommaire |
|
Pratique des tests Statistiques La fiche contient quelques exercices portant sur les tests statistiques paramétriques ou non à réaliser sous le logiciel R. |
|
Comparaisons de deux moyennes avec le test paramétrique de Student (test $t$) Cette fiche donne un exemple simple, complet et reproductible d'un test de comparaison de deux moyennes avec le test $t$ de Student. Elle suit un mode opératoire classique où l'on cherche à vérifier que les conditions d'application du test sont réunies. Elle utilise volontairement une syntaxe de Rlogo{} suggérant que des généralisations de l'approche sont possibles. Deux exercices d'application sont proposés. | 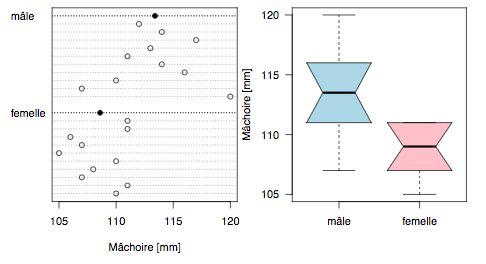 |
|
Comparaisons de deux moyennes avec le test non-paramétrique de Wilcoxon-Mann-Whitney Cette fiche donne un exemple simple, complet et reproductible d'un test de comparaison de deux moyennes avec le test non-paramétrique de bsc{Wilcoxon-Mann-Whitney} (cas particulier du test de bsc{Kruskal-Wallis} quand on n'a que deux échantillons). Deux exercices d'application sont proposés. |
|
Comparaisons de moyennes Le test de Shapiro et Wilks. Le test de Bartlett. Normalité et variances égales. Non normalité. La loi de Wilcoxon. Exercices : choisir un test. |
|
Choisir un test Corrigés d'exercices de la fiche tdr31 |
|
Taux de G+C des chromosomes bactériens Examen et solution, BMS 2002 |
|
Simulation avec un peu de programmation : la plus longue suite Examen Magister (2002) statistiques non-paramétriques (avec solutions) |  |
|
Variables Estudiantines (examen de contrôle continu depuis 2003) Une initiation de niveau L3 visant à familiariser les étudiants aux problèmes concrets rencontrés lors d'une analyse statistique dans la vraie vie : vous allez analyser vos propres données (Yes!). On part de la mesure et de la saisie des données sur la promotion actuelle, puis, via l'importation des données des maudites promotions précédentes, on rédige un rapport reproductible sur une problématique donnée. Le choix de la problématique est libre à ce niveau, l'originalité est encouragée (si elle est reproductible). |
|
Variables Estudiantines (examen de contrôle continu depuis 2003) Aucun sommaire |
|
Quelques tests liés aux variables discrètes Khi2 de contingence, test exact de Fisher, test de McNemar : quelques exemples |
|
Analyses de la variance Bases du modèle linéaire à effet fixe : régression simple, analyse de variance, régression multiple, analyse de covariance |
|
Allométrie pour les nuls Ce document est une introduction tout en douceur aux concepts de l'allométrie avec plusieurs niveaux de lecture. Il y a beaucoup de latin (du code Rlogo{}). Passez outre en première approche ! Umberto Eco a écrit dans l'Apostille au Nom de la rose qu'un jeune garçon de dix-sept ans lui a dit qu'il n'avait rien compris aux discussions théologiques mais qu'elles agissaient comme des prolongements du labyrinthe spatial. Par rapport au latin, les exemples de Rlogo{} sont reproductibles. |  |
|
Arrachage de clous et sous-espaces vectoriels La fiche donne quelques éléments de réflexions sur la manipulation des modèles linéaires à partir d'un exemple de P. Dagnelie. L'emploi des facteurs à modalités ordonnées dans une analyse de variance ne pose pas de problèmes particuliers aux utilisateurs. |
|
Le fleuve Vam Co Tay : espace-temps sans répétition La fiche traite un exemple de données hydrobiologiques avec une mesure par date et par station. On utilise le modèle linéaire pour classer les variables par type de modèles spatio-temporels |  |
|
Tailles des testicules et systèmes d'appariement Aucun sommaire |
|
Densité de population et ingestion de nourriture chez un insecte vecteur de la maladie de Chagas La fiche permet de se familiariser avec la planification et l'analyse expérimentale. Les questions biologiques auxquelles nous devons répondre nécessitent une planification expérimentale rigoureuse et l'utilisation d'outils statistiques adaptés comme le test de Levène et l'Analyse de variance (ANOVA). Les données présentées sont issues d'une étude de collègues argentins avec qui nous collaborons : E H. Weir, J.E. Rabinovich et Martin Torres. Les données utilisées dans cette fiche ne représentent qu'une petite partie des données originales. |
|
Modèles linéaires généralisés Erreur de bernoulli et lien logit, erreur normale et lien identité. Erreur binomiale, erreur poissonienne. Déviances. Modéliser une présence-absence. |
